Research
Most of my published papers can be found here and technical reports can be found here.Retrospective
Generally speaking, I've worked on the design and implementation of call-by-value and mostly functional programming languages, early on with LISP and then Scheme and later with the Standard ML and OCaml dialects of Robin Milner's beautiful ML programming language. I was drawn to languages of this kind after I was introduced to LISP 1.5 in a wonderful class on programming languages taught by a graduate student at Indiana University in the summer of 1977. Since then, my work has ranged from concrete implementation-oriented issues that arise in optimizing compilers to more theoretical aspects of programming languages.From my perspective, three of my projects/collaborations are worth highlighting.
1. Type-Directed Compilation with Flow Types
This work was carried out as the principal focus of the Church Project during my tenure as an Assistant Professor. It was published in a number of articles, most notably in a 2002 JFP article A calculus with polymorphic and polyvariant flow types, joint with Joe Wells, Lyn Turbak and Allyn Dimock.
In the summer of 1995 I attended a talk by
Trevor Jim on
principal typings.
Subsequent conversations with my PhD advisor
Assaf Kfoury,
Joe Wells and Lyn Turbak led to the
establishment of the Church Project in August of 1995, a joint research
project between Boston University, Wellesley College and Boston College.
The central focus of the Church Project was the design and development
of a typed intermediate language (TIL) that might be used in a reliable
optimizing compiler for ML-like programming languages. The advantage
of a typed IL over an untyped one is that the compiler can
type-check the intermediate representation (IR) after transformation
steps to ensure that program invariants have been preserved.
The particular TIL developed in the Church Project introduced a
novel type system with interesection and union types together with
flow labels. This enables a compiler to track the flow of values
from their creation sites (sources) to their consumption sites
(sinks) and to customize data representations in a safe and flexible
way. For example, the following snippet of code
produces a 3-tuple as a value, using 3 principal functions k, g and h. The example illustrates non-trivial flow of these functions to various call sites. In the IR, the program is represented with explicit types decorated with integer flow labels.
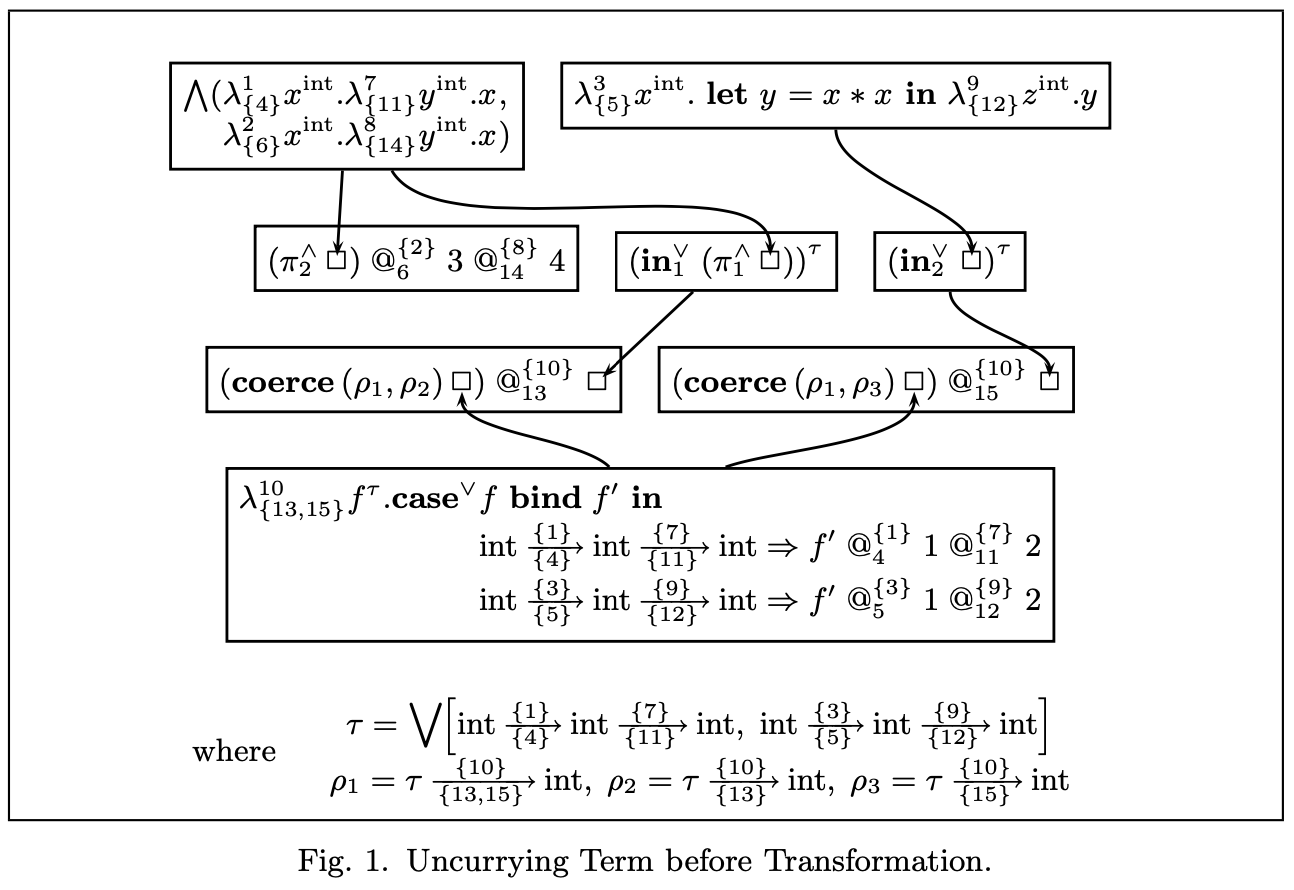
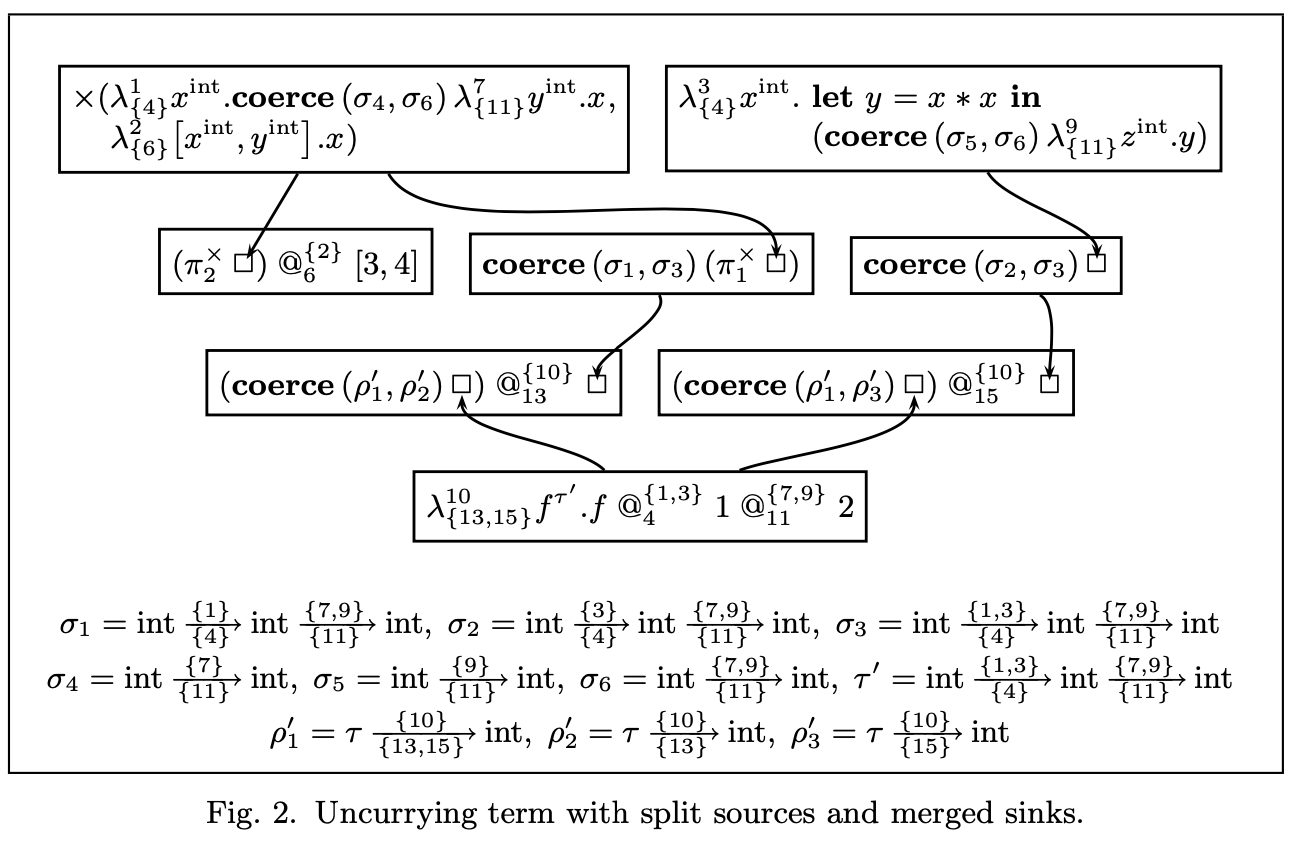
In the diagram, arrows represent flow. The function k can flow to two different call sites: site 4 or site 6. The function is represented as a virtual 2-tuple of intersection type. This allows the compiler the option of generating two different copies of k in a type-safe manner. The compiler can choose to reify the virtual 2-tuple into a real heap-allocated 2-tuple in the object code. This process is called source splitting.
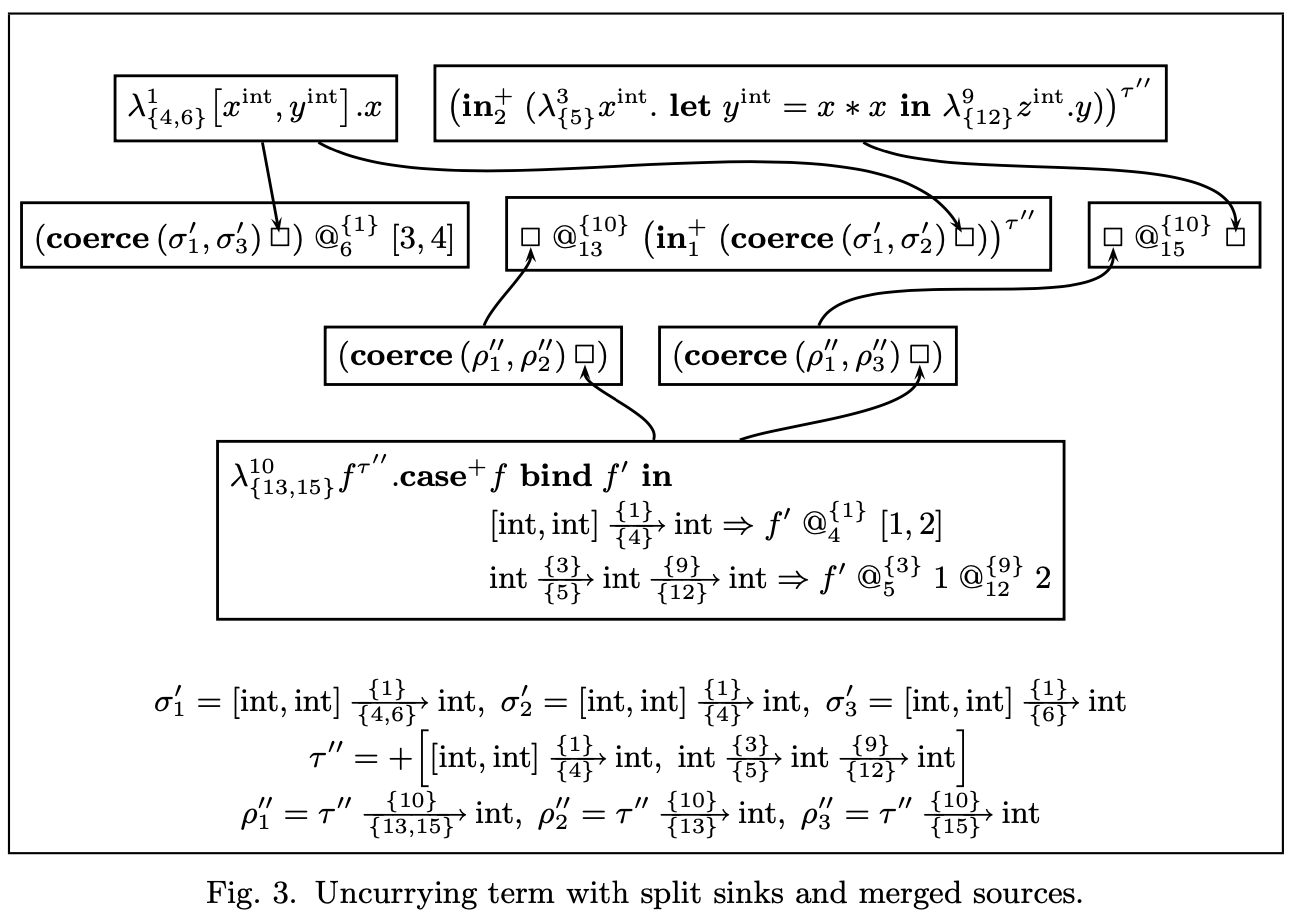
The type system also allows the compiler to perform sink splitting by reifying virtual case dispatches to real case dispatches in the object code.
2. An Effectful Type System with Storage Annotations for Interprocedural Allocation
This was joint with Torben Amtoft, then a postdoc working with the Church Project. Virtually all of the heavy lifting in this project was done by Torben Amtoft who came to this work with extensive experience with effect systems. This work was published in Inferring annotated types for inter-procedural register allocation with constructor flattening which appeared in the proceedings the 2003 Workshop on Types in Language Design and Implementation (TLDI). In retrospect, this paper should have been submitted to a major conference such as PLDI or ICFP where it likely would have had greater impact.Consider the code snippet
In the example on the left, the type t1 denotes a heap-allocated
record where the integer fields a and b are allocated in
consecutive memory words. The base address of the block of memory is
allocated in virtual register r1. In the example on the right,
the type t1 denotes the same record but with no allocation at
all – the fields of the record are allocated directly in virtual
registers r1 and r2.
The type system is proven sound so any typing gives rise to consistent
execution.
3. Sorting Out LISP's Metalinguistic Power
This work was carried out as the principal focus of my PhD thesis at Boston University under the direction of Assaf Kfoury with additional advising by Mitch Wand. It was published in a 1992 TOPLAS article M-LISP: A representation-independent dialect of LISP with reduction semantics.
Programming in LISP is great fun! Symbolic expressions
(S-expressions) are the ultimate flexible recursive data structures,
immutability is the default and, since everything is an S-expression,
it's fairly easy to write meta-programs – programs that work on
the representations of other programs.
But something seems a little fishy – how can the form
(bobcat deer bear) be a list while the form
(find bobcat bobcats) is a function call? This was
the question put to me by Mitch Wand when I was a graduate student in
1987. I spent untold hours thinking about this puzzle. The answer
came to me in a flash one morning in the summer of 1988 –
there is a simple error in the original definition LISP. (!)
The error appears on page 15 of John McCarthy's
seminal 1960 paper introducing LISP: Recursive Functions of Symbolic Expressions and Their Computation by Machine.
The error, highlighted above, was subsequently propagated into all derivative
dialects of LISP including Scheme and Racket. Correcting the
error and tidying up the downstream consequences leads to a simpler
programming language but the metalinguistic power is lost. The
details are laid out in the aforementioned TOPLAS article.